I have a long-term, on-again-off-again, troubled relationship with poetry. When it’s good with her, it’s amazing. My brainflubbers tingle like firecrackers, my heart hyperbolically hiccups, and the raw, elusive connections between everything tug at me like the leash on my lunge-happy dog. But then poetry leaves me penniless and depressed and I start wondering if every wonderful feeling I’ve had with her has actually been a form of psychosis.
Thus I was surprised this week, while knee deep in the dark overlords’ Large Language Models (LLMs), that I came across something strange. Those transcendent sparks she set off were not my imagination. For in the blueprints of LLMs, one can make out poetry’s mathematical validation
Thanks for reading! Subscribe for free to receive new posts and support my work.Subscribed
Let me explain. But first, let me assure you I am not going to talk about LLM-generated poetry, which to me, seems to have very little to do with the written artifacts produced by the cognitive witchery of poetic practice. Nor am I going to talk about whether everything in the world can just be explained away with a mathematical equation as long as the equator that includes Egyptian hieroglyphs and Wingbat font. I don’t care about those things. Sorry.
What I do find fascinating, though, is that in a strange, spiraling way, poets have been doing Stephen Hawking-level math for thousands of years — but with squirmy, slippery animals called words. Without a single unit of processing power, they’ve intuited something eerily similar to the thing at the heart of today’s most advanced language models: that meaning isn’t fixed, it’s relational. A word doesn’t mean something in isolation — it means something in context, through its shifting constellation of relationships to everything around it.
This is how LLMs learn to “understand” language. It’s also how many poets describe what they do when they create a poem. But while both work from the same insight, they apply it very differently. And those differences raise head scratching questions about the tension between what we’ve already learned how to say and what we’re still trying to.
So roll up your sleeves. Grab something salty and crunchy. We’re going in.
Computersplaining Meaning
An LLM’s ability to perform comprehension and intelligent speech is based on something called semantic space. I say perform, because unless you are Blake Lemoine, most of us human folk don’t think LLMs are actually comprehending. Anyway, you can think of this semantic space as an LLM’s dictionary, except instead of each word having concrete definitions, each word is defined solely by their relationship to every single other word in that semantic space. Below is a picture of an LLM with their semantic space dictionary.

Semantic spaces are dimensional. ChatGPT-4, for example, has a semantic space of 16,000 dimensions. My brain is an old model, so I haven’t had much luck trying to image 16,000 dimensions. For me, it was easier to understand this concept by starting with a two-dimensional semantic space, one that we can represent with an x axis and y axis. (Yay, middle school math!) Let’s say this two-dimensional semantic space contained the following words:
- ice cube
- milk
- cat
- human body
- pizza box
- coffee
- refrigerator
- car engine
- oven
Now, say we wanted to plot these words according to the average size and temperature of the objects they represent. We would turn size and temperature into dimensions, with the X axis representing the size dimension, and the Y axis representing the temperature dimension. Then we would plot the words according to these two qualities.
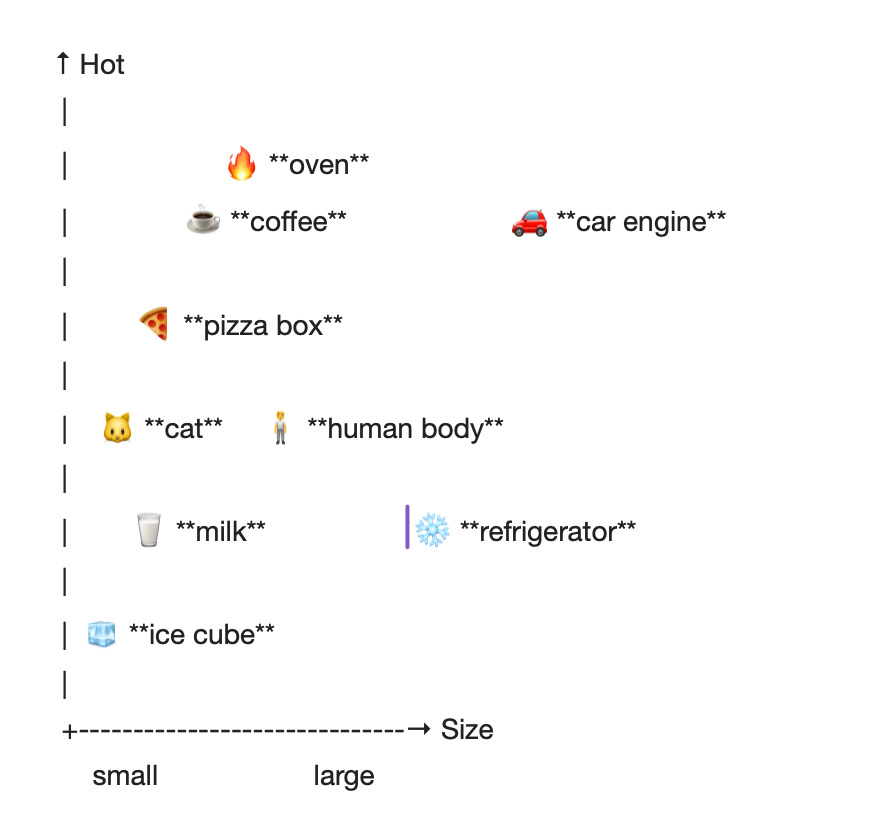
Take a look at where all the words are positioned. The ice cube, for example, is at the lower-left of the chart because it scores low on both the X-axis (size) and the Y-axis (temperature). It’s small and cold. The oven, by contrast, is in the upper-right of the graph, where the X-axis stretches toward large and the Y-axis toward hot. The distance between words in either dimension indicates the similarity between them in the context of the attribute represented by that dimension. Hooray! You understand two dimensional semantic space!
Now, let’s add another dimension. This dimension will indicate the average lifespan of the object represented by each word. Each of our words will preserve their original x and y position, but will now also have a z position that represents how long it takes that object to shuffle off its mortal coil. Below is our three dimensional graph, just like the 3D boxes you learned to draw in grade school. We got this!
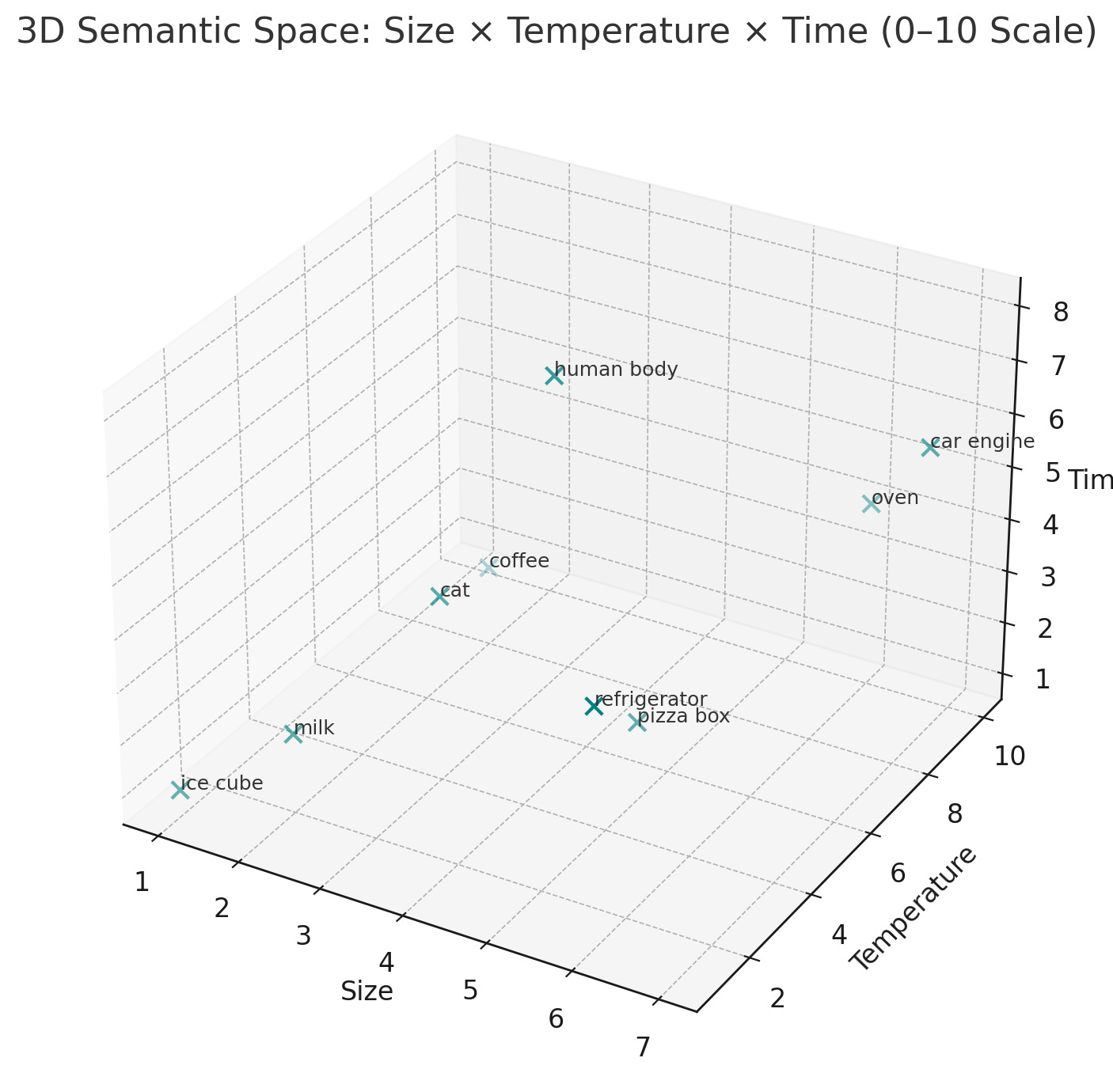
Ok, my words are plotted in completely non-sensical places because I don’t want to fiddle with this graph any longer, but you get the idea! A word’s location in this three dimensional space encodes its size, its temperature, and its average lifespan. But of course, any word has far more than three attributes. In fact, you might say, they have an indefinite number attributes. You could describe the objects represented by these words in terms of their color, their purpose, or the likelihood of being defunded! To capture any of these attributes, you would simply assign them a dimension. A dimension for apocalypseness! Microwaveability! Crunchiness! As many dimensions as you like. So even though we can’t visually depict 16,000 dimensions, we can appreciate what that dimensionality means.
Except one thing. There are no words in an LLM’s semantic space. Not even a single letter. Not even for the dimensions themselves, which aren’t labeled “hot” or “cold,” “angry” or “fuzzy,” but are just . . . also numbers. A word’s meaning is pinned to a position in this space, not because it has a definition, but because of how it behaves in relation to all the other words it’s seen before.
So who decide where to plot the words in this 16,000 dimensional landscape? Meet the transformer.
Turning Words Into Numbers
I was surprised too, but essentially, every LLM learns to read and write from this guy. A transformer.

Kidding, but actually the image is useful. At least for me because it’s hard to otherwise imagine something defined as “a model that builds meaning by calculating how each word relates to every other word in context.” So let’s do what humans have done since the dawn of time to grok inexplicable things and turn our transformer model into a human-like creature! Now that we have a nice anthropomorphized vision of a transformer, we can try to understand how he turns eleventy billion words in to a shiny new semantic space.
Kidding — but honestly, the image helps. It’s hard, at least for me, to wrap your head around something defined as “a model that builds meaning by calculating how each word relates to every other word in context.” So let’s do what humans have always done when faced with the inexplicable: turn it into something humanish. Now that we have a nicely anthropomorphized transformer to work with, we can start to understand how he chews through eleventy billion words and plops them out into shiny new semantic space.
But before our little language beast can start building meaning, he needs something to chew on. And not words — he’s not that kind of monster. He only eats numbers. So, you should be asking yourself, after Sam Altman stuffs his breeches with everybody’s ABCs and drives off into the sunset, how are they turned into numbers? It’s quite easy actually. All we have to do is take our eleventy billion words of training data and convert them into a form he can digest. That means running the text through a program called a tokenizer, which slices everything up into tiny, learnable chunks like “un,” “believ,” “able.” These chunks are called tokens, and they let the model build a flexible “vocabulary” — a set of reusable building blocks that can represent virtually every word in the dataset without needing to memorize them all. For instance, it’s estimated that ChatGPT-4 was trained on 3.25 trillion words, but its vocabulary is just 100,256 tokens. Tokenization is its own kind of magic, but our transformer doesn’t eat tokens. He eats vectors. So let’s keep moving.
Next, each token gets a unique ID. Think of the ID like a row number in a spreadsheet. The number itself doesn’t mean anything; it’s just a way for the model to keep track of each token. Then, each ID is assigned not one, but three vectors. These vectors are long lists of numbers that describe the token’s location in a massive, multi-dimensional semantic space.
In case you don’t know what a vector is, it’s simply a list of numbers between two square brackets, like this:
[8, 5, 9, 4]
The vector above has just 4 numbers, but in training, vectors typically have hundreds — sometimes thousands. Each number corresponds to one dimension in the model’s semantic space. As mentioned earlier, ChatGPT-4’s semantic space has 16,000 dimensions, which means each vector used during training contains 16,000 numbers. And since every token gets three of these vectors… well, we’re now dealing with 100,256 tokens, times three vectors, times 16,000 numbers. That’s a lot of math. (Don’t worry — we’re not going to multiply it.)
At the very beginning of training, the values in those vectors are completely random. But as training begins, the transformer starts adjusting them: gently nudging each token into a spot that reflects how it behaves in context. “Un” learns to orbit verbs like “do” and “see,” while “frig” slowly settles near other appliance-sounding syllables. This process doesn’t give the model a dictionary definition. Instead, it generates a relational fingerprint of all the tokens it’s trained on. It learns what a word means by learning how much it matters to the words around it. The math behind this is called attention, and it’s how the model decides to organize its semantic space. (If you’re interested in a supercyberlicious write up of the math, let me know, and I’ll consider posting the gigantic explanation I just deleted from this post. It’s actually pretty neat.)
So the transformer is a machine that builds meaning not from rules or definitions, but from relationships. During training, its semantic map is constantly adjusting, nudging tokens around to reflect more precise patterns of use. But the transformer wasn’t built to transform forever. Once training ends, the map is frozen. It becomes the model’s permanent reference for predicting what comes next, whether in a chatbot, a code assistant, or a talking toaster.
And yet, there’s something relevant about this model to the way humans use language, especially its understanding of meaning as context, not definition. But unlike the transformer, we aren’t bound to a single training set. We move through an evolving wilderness where each linguistic encounter can disrupt, reroute, or rewire our internal map. Our semantic space stays liquid. We can keep transforming. And sometimes, in moments of rupture, attention, or beauty — we do.
That’s what got me drunk texting poetry again at 2 a.m. Heyyy.
Our Little Map Breaker
Once a transformer has seen enough words, everything starts to settle. Meaning settles. The space settles. It gets very good at knowing what you probably meant, what people usually say, what comes next. And we do this too in our speech and our thoughts. We repeat what works. We let our semantic maps crystallize. Nothing surprises. Nothing slips.
This isn’t necessarily bad. Sometimes I wish I was a better stochastic parrot, because then maybe I wouldn’t ramble so much during work meetings or add twenty extra phonemes to the word anthropocentric while talking to my philosopher husband. But when it comes to making meaning out of the wilderness of human experience, a frozen map doesn’t cut it. It occludes our capacity to say what isn’t represented, to reach towards saying the unknown. It becomes a linguistic prison.
While a transformer calculates what is likely, a poem often leaps for what is unthinkable but barely sayable. It forges connections between words that ought not to belong together, yet suddenly do. In doing so, it creates new gravity wells in meaning-space, pulling distant words into relation and insisting, through rhythm or feeling, that they hum. It stretches the possible meanings of a word in order to trace the unsayable.
In her essay Some Notes on Organic Form, the poet Denise Levertov describes how meaning in a poem arises not from isolated words, but from the unfolding relationships between them: a dynamic, recursive process shaped by memory and movement. As she puts it: “A may lead to E directly through B, C, and D: but if then there is the sharp remembrance or revisioning of A, this return must find its metric counterpart…”
Her description of poetry is that of a transformer that redraws the semantic map as it learns it.
If you can’t tell already, I think LLMs are impressive and intriguing. But their math proves that poetry, no doubt, is still the superior technology. I hope she texts me back.